How to Create a Basic Content Based Recommendation System

In the world of internet, the advent of e-commerce had opened many new areas of research for computer science. One of such areas is emarketing, i.e. advertising items online and recommending some items to the user, so that they can purchase more items.

In this blog post, we will describe the process of creating a basic content based recommender system.

Background

A Recommender system is a computer program that helps a user to find items and content by foreseeing the user’s rating of each item and demonstrating to them the items that they would rate exceedingly. The process works by predicting the rating for an unrated item by the user, based on some parameters and characteristics of either item or user profile or both. The prediction can also be based on ratings by other similar users or ratings for other similar products.

Developing a good enough recommendation system has been one of the greatest area of R&D for computer science. Since the evolution of Data Science and Machine Learning, tons of approaches to develop such system. However the two basic kinds of recommendation systems are

For this blog we have the following objective

Objective

On the basis of item’s characteristics and user’s preference, we will predict the user’s rating for all items that were unrated by the user.

Data Source

We will be referring to the movielens latest (1 MB) database (http://files.grouplens.org/datasets/movielens/ml-1m.zip, an online, free to use, database for movie ratings). Therefore, the term “items” here refers to movies, and users are those who watch movies and have rated at-least one movie.

Data Definition

We are going to use selective files from the dataset, so below we define the files we will be using

1. movies.csv:  A comma separated file, containing movie profiles (describing movieId,title and genres). Genres are pipe separated values, denoting the category of each movie. For now, we will be using genres only, as a relevant characteristic of movies for predicting ratings.
2. ratings.csv:  A comma separated file, containing information about which user has rated which movie (describing userId, movieId, rating and timestamp). We will be using userId, movieId and rating columns for creating user profiles.
3. We will not be using any other file.

Abstract

From movielens data, we have observations of users ratings for different movies, where each movie has some features associated with it. These features are the genre of the movie, which indicate the actual categories of the movie.

However we notice that there are many users who have not rated many movies yet, but we also see that these users have already rated some of the movies. This content recommender system predicts these missing ratings based on the features of movies and preference of individual users. For example if a user has already rated some action-romance movies highly, we can infer that this user may also like other action-romance movies. This inference or prediction can help us recommending users the movies that they have not rated yet.

In Machine Learning terms, this is a regression problem, where we have a user preference or utility matrix Y, and a movie features matrix X. Y is having some unknown values, so based on X and Y, we train a model to find weights W. Using these weights we will be able to predict the missing movie ratings.

Working

From the above definitions, consider we have a large matrix, where each cell identifies an individual rating for a movie (rows for movies, columns for users, cell values as ratings). For example, a sub-matrix of it could be

here Movie 1 to Movie 3 are movies and User 1 to User 3 are users, ‘?‘ denote an unrated cell, while numeric values denote individual ratings. We have to predict the values for these ‘?’. Let’s call this matrix the utility matrix, and for simplicity, replace ‘?’ with 0 to indicate that this user has not rated the movie. Similarly, consider another matrix, where we map each genre against each movie. We have total 20 distinct genres from the dataset. For example, a sub-matrix could be

here Movie 1 to Movie 3 are movies and on columns are genres, where each individual cell refers to a boolean integer, denoting if a movie belongs to this genre (1) or not (0). Let’s call this matrix a features matrix. Now, this is a regression problem, where we have to predict the rating, given the features matrix and existing ratings matrix (i.e. utility matrix). We will train a model over this data to find a theta/weights matrix, such that by using weights matrix we can predict new ratings. From now-on consider following symbols for convenience

X = features matrix

Y = utility matrix

W = thetas/weights matrix

u = number of users

n = number of features

m = number of movies

We will train the model for X given Y to find W. After we have computed W, we will be able to find the prediction matrix Ŷ (containing the approximate predicted ratings), where

Ŷ = X * W

or

Ŷ = W^T X

* depends on the dimensions of these matrices

The process of training the model will be as follows

1. Create a random W matrix of size u x n
2. Add a bias term to W, say it w₀ and have it equal to 1, now W is of size u x (n + 1)
3. Add an intercept term to X, say it x₀ and have it equal to 1 (now the first column of X will be all ones, and dimension will be m x (n + 1))
4. The prediction function for this problem is Ŷ =h_w(x) = w₀x₀+ w₁x₁+ … w_nx_n = W^TX
5. Create a cost function (the optimization objective) for regression based on least squared errors to compute the cost of the model. The cost function may look similar to   
6. Create a function to compute the gradient of this cost function
7. Apply batch gradient descent algorithm iteratively to identify new weights (W), until weights stop changing.
8. The final weights will be used for predicting new ratings based on the formula Ŷ = X*W

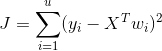
If you want to know how the above model has performed

1. Take the element wise difference between Y and Ŷ, you will get an error matrix
2. On error matrix, take element-wise squares and divide each element by 2
3. Sum all rows and columns and divide by the number of movies to get the real valued error

You may use this error to judge how well your model has performed.

Congratulations, at this moment you have understood how to create a basic content recommender system.

Further notes

This is just a basic recommender system, you may dig in further to optimize this by adding, for example, new features using features engineering, or you may use regularization, or even gather more data. It’s all up to you, how you want the predictions to take place.

Blog Post